[Downloads]

Nanoskalige Dimensionen werden weltweit mehr und mehr industriell erobert, nachdem sich die Zugriffsmöglichkeiten auf die einzelnen Bausteine der Materie in den letzten Jahrzehnten wesentlich verbessert haben. Das Zentrum für Computational Nanoscience (CNS), als Bestandteil des Interdisziplinären Zentrums für Materialwissenschaften, wid-met sich der theoretischen Untersuchung, Modellierung und Simulation von Nanosystemen. Dabei besteht die größte Herausforderung darin, Modellierungen über mehrere Größenordnungen von Raum und Zeit durchzuführen.

Nanostrukturen auf Metall- Oberflächen
Die Möglichkeit metallische Nanostrukturen auf Metalloberflächen direkt zu untersuchen und gezielt zu verändern, erfordert eine kritische Prüfung klassischer Konzepte. In Zusammenarbeit mit Prof. Dr. V.S. Stepanyuk und Prof. Dr. J. Kirschner vom MPI für Mikrostrukturphysik wurde das Konzept der mesoskopischen Fehlpassung erarbeitet, welches erfolgreich zur Diskussion der Eigenschaften metallischer Nanostrukturen eingesetzt wird.

Begriff der Fehlpassung für Nanostrukturen
Ausgehend von der Gitterfehlpassung, d.h. dem Unterschied der Gitterkonstanten von Substrat und dem Material aus dem die deponierten Nanostrukturen bestehen, kann man überlegen, welche mechanischen Spannungen beim Aufwachsen der Nanostrukturen auftreten.
Diese Überlegungen versagen jedoch oft bereits auf qualitativem Niveau! Die Anwendung des klassischen Begriffs der Gitterfehlpassung auf den Beginn des epitaktischen Wachstums führt nicht zu einer sinnvollen Beschreibung der resultierenden Spannungen. Die makroskopische Fehlpassung wird aus den Gitterkonstanten der Volumenkristalle berechnet. Die Differenz der Gitterkonstanten wird ins Verhältnis zur Substratgitterkonstante gesetzt. Für die Homoepitaxie ist die makroskopische Fehlpassung null. Dieses einfache Bild ist jedoch nicht zutreffend. Auch bei der Homoepitaxie treten Spannungen auf. Es kommt zu atomaren Verschiebungen, die für die Wachstumsform, Insel- oder Lagenwachstum, entscheidend sein können.
Die Spannungseffekte auf mesoskopischer Skala können nicht mehr mit der makroskopischen Fehlpassung diskutiert werden, da die mittlere Bindungslänge in der wachsenden Nanostruktur von der Bindungslänge im entsprechenden Volumenkristall verschieden ist.

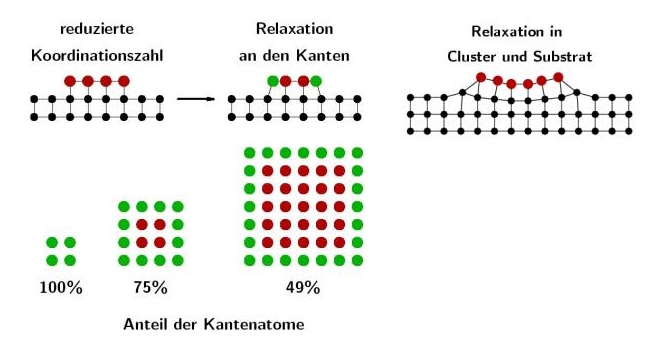
Abb.1: Ursache der mesoskopischen Gitterfehlpassung

Die Notwendigkeit der Anpassung der Beschreibung auf der Nanoskala wird aus Abb. 1 klar. An den Rändern der Inseln treten auf Grund der verringerten Koordinationszahl starke Relaxationen auf, die mit zunehmendem Abstand vom Inselrand kleiner werden. Das Skalenverhalten der Fehlpassung wird maßgeblich durch das Verhältnis der Anzahl der Randatome zur Gesamtzahl der Atome bestimmt.
Bei der Definition der mesoskopischen Fehlpassung wird die mittlere Bindungslänge in der Nanostruktur ins Verhältnis zur Bindungslänge im Substrat gesetzt. Die mesoskopische Gitterfehlpassung kann nicht einfach aus den Gleichgewichtsgitterkonstanten bestimmt werden, sondern erfordert numerische Simulationen. Für kleine Inseln variiert die mesoskopische Gitterfehlpassung stark mit der Zahl der Atome in der Insel.

Inselformen - Käseglocke oder Untertasse
Aus Rechnungen folgt, dass die Cu-Insel auf einem Cu(001)-Substrat die Form einer "Käseglocke" annimmt, d.h. die Randatome relaxieren stärker in Richtung der Cu Oberfläche als die Atome im Zentrum der Insel. Auch das Substrat zeigt deutliche Relaxationseffekte. (s. Abb. 2) Im Falle des heteroepitaktischen Wachstums von Co auf Cu(100) kommt es zu vergleichbaren Relaxationseffekten. Jedoch zeigt die Insel eine "Untertassenform".
Weiterhin stellt man fest, dass Relaxationseffekte hier größer sind, als beim homoepitaktischen Wachstum von Cu-Inseln auf Cu(100).
Die Unterschiede in den Inselformen sind in den unterschiedlichen Kraftwirkungen der Atome aufeinander begründet. Für die Untertassenform der Co-Inseln ist auch der Magnetismus dieser Nanostrukturen mit verantwortlich.

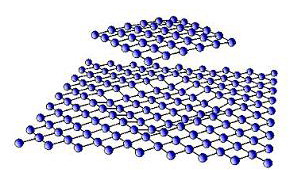
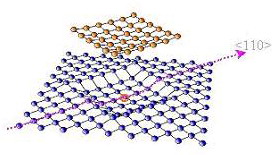
Insel aus Cu-Atomen	Inseln aus Co-Atomen
Abb.2: Quadratische Inseln (36) Atome auf Cu(001)

Photonische Kristalle
Photonische Kristalle sind im (sub)- µ-Bereich periodisch strukturierte dielektrische Materialien. Solche periodischen Strukturen können Frequenzbereiche (Bandlücken) aufweisen, in denen sie kein Licht transmittieren. Photonische Kristalle kann man auch als Halbleiter für Licht bezeichnen.
Solche photonischen Kristalle sind die Basis für vielfältige Anwendungen in der Optoelektronik. Sie werden in optischen Technologien, die die heutigen Informationstechnologien ablösen werden, eine große Rolle spielen. (s. Abb. 3)
Am MPI für Mikrostrukturphysik werden in der Abteilung von Prof. Dr. U. Gösele zweidimensionale Strukturen, bestehend aus gitterperiodisch angeordneten Poren im Ausgangsmaterial, z.B. einem Silizium-Wafer, mittels elektrochemischer Ätzverfahren hergestellt.

Abb.3:Photonic Micropolis - Vision einer Kombination verschiedener auf photonischen Kristallen beruhender Komponenten (Joannopulos Research Group at MIT)

Diese Strukturen können als Template zur Herstellung von Nanoröhren und Nanostäben, wie in einem anderen Artikel erläutert, verwendet werden, stellen aber gleichzeitig photonische Kristalle dar. Eine wichtige Problemstellung ist die Optimierung der photonischen Bandlücke in zweidimensionalen Strukturen, bzw. die Konstruktion von dreidimensionalen photonischen Strukturen mit großer photonischer Bandlücke. In Zusammenarbeit mit Dr. R. Hillebrand (MPI für Mikrostrukturphysik) wurde eine dreidimensionale Struktur entwickelt (s. Abb. 4), die eine photonische Bandlücke von mehr als 25% der Mittenfrequenz der Bandlücke aufweist.

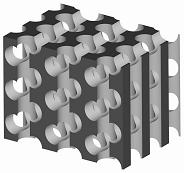
Abb.4: Design eines photonischen Kristalls
basierend auf makroporösen Silizium

Diese Struktur kann aus den elektrochemisch hergestellten zweidimensionalen Strukturen erzeugt werden, indem senkrecht zu den geätzten Poren ein weiteres Porengitter mittels Ionenstrahlätzung erzeugt wird.
Gerade dieses Beispiel zeigt die Zukunft des Gebietes Computational Nanosience: das gezielte Konstruieren von Mikro- und Nanostrukturen mit bestimmten vorgegebenen Eigenschaften.

Wolfram Hergert