Abstract

    The theoretical fundamentals for the calculation of the local cathodoluminescence (CL) signal and electron beam induced current (EBIC) in the scanning electron microscope (SEM) are outlined. Especially, the simulation of the signal contrast profile behavior of individual dislocation configurations is reviewed. Existing analytical models and new numerical approaches are summarized.
    Besides the evaluation of material parameters, the conception of combined SEM-CL/EBIC is applied for the quantitative experimental characterization of single defects in grown-in, misfit as well as glide dislocation structures with respect to their recombination activity in various III-V semiconductors. Recent CL data from dislocations in GaP, GaAs, and CdTe in the low-temperature range are analyzed in the framework of temperature-dependent defect-related recombination kinetics.

Introduction

    During the last decades, scanning electron microscopy (SEM) has been developed towards a standard experimental method to obtain images from a large variety of materials. In semiconductor characterization and research, the investigation of local electronic and optical properties is of vital importance for problems ranging from micro- and optoelectronic materials, devices, and quantum structures to solar cells. Here, both cathodoluminescence (CL) and electron beam induced current (EBIC) mode have been successfully applied [1,3,4,25,50,59,74] since they allow access to a defined specimen bulk region due to the beam-induced creation of electron-hole pairs. Besides the very important aspect of imaging and identification of particular features (electrically and optically active dislocations, precipitates, stacking faults, microdefects etc.) with high lateral resolution, combined SEM-CL/EBIC offers the possibility to determine reliable quantitative information on relevant local electronic and optical material parameters [39] and, especially, the recombination behavior at individual defects such as dislocations [62]. This purpose, however, requires an accurate simulation of the signals as a function of these parameters. The corresponding equations must also be related to the carrier recombination processes at the defect. Although this is a complex task in general, it may be largely simplified in many practical cases or even performed analytically. The appropriate model functions are then fitted to the experimental data, and the material parameter values are derived.
    If we follow a strategic scheme for performing quantitative SEM-CL/EBIC investigations such as that given in Table 1, it is possible to obtain important information about the electronic properties and defect recombination activity which are significant for the treatment of many semiconductor defect physics problems. The sui tability of the given strategy will be demonstrated by several theoretical and experimental examples in this paper. Some aspects of this scheme should be emphasized at this point. Investigations of the semiconductor matrix properties are a necessary prerequisite for the quantitative study of defects and their electrical activity. Under these conditions, a complete set of matrix and defect parameters may be obtained from combined CL/EBIC measurements. This requires, however, comprehensive simulation models on one hand and information about the structure and configuration of the extended defects on the other. The knowledge about the carrier recombination processes is important for a correct interpretation of the experiments. While bulk recombination paths in semiconductors are generally known, the identification of the defect recombination mechanisms is a primary aim of these studies. Especially, the temperature dependence of dislocation recombination and the recombination kinetics when state occupation is changed by varying the injection level should be correlated with structural details such as the interaction with point defects and models about electronic states in the dislocation core and the surrounding region.
    In this paper, we will restrict ourselves to an outline of the theoretical fundamentals for basic defect geometries such as a single dislocation in a thick epilayer or bulk sample with the aim of a quantitative experimental evaluation of corresponding model defect systems by combined CL and EBIC. We will follow the widely accepted generalized theoretical conception by Donolato, Pasemann, and Hergert [11,14,21,28,45,47,49]. The large variety of results from mainly qualitative investigations using CL or EBIC, detailed calculations for particular geometries as well as special aspects concerning quantum structures, devices or instrumentation are largely beyond the scope of our review. The interested reader is referred to some of the reviews cited above.

Theoretical Fundamentals

    Figure 1 contains schematically the various carrier and photonic processes occurring in CL and EBIC experiments in the SEM. The carrier behavior is primarily represented by the electron-hole pair generation distribution g(r), the minority carrier diffusion length , and the radiative and non-radiative bulk lifetimes r and nr which determine the corresponding recombination rates Rr and Rnr. The continuity equation for the time-dependent excess minority carrier density q(r,t) is established as the balance of diffusion and drift currents, total recombination, and beam induced generation rates1 at each point r of the sample:

where the total minority carrier lifetime (r) = (r-1 + nr-1)-1 is generally considered as a defect-related function of the location r, D is the diffusion coefficient, and µ the minority carrier mobility. The validity of (1) requires a linear recombination model such as band-to-band recombination in the low-injection regime (e. g., q = p « n0 for an extrinsic n-type semiconductor) so that the majority carriers do not need to be considered. If electric fields E(r,t) can be neglected in a neutral bulk semiconductor, the stationary balance (p/t = 0) is described by the steady-state continuity diffusion equation
According to the actual sample geometry, boundary conditions have to be fulfilled such as
for any surface or interface rS where a normal diffusion current is linked to a non-radiative surface/interface recombination velocity vS. In directions with practically infinite sample extensions, the carrier density must vanish (q(r)  0 for r  ).
    For the generation rate, various models have been used in the literature. For the given partial differential equation of Helmholtz type, a delta-function point source leads to the determination of Green's function G(r,r'). It can be obtained using the method of mirror images [11] for various defect-free sample geometries. Due to its mathematical simplicity, a uniform sphere generation also allows the determination of q0(r) for the homogeneous half-infinite sample in analytical form [22]. For a correct quantitative analysis of experimental data, however, the use of a realistic generation distribution g(r;Ub) = G0 gr(r,z) gz(z) is essential (G0 is the total carrier generation rate). It can be obtained by Monte Carlo (MC) simulation of scattering and energy dissipation of primary electrons of energy eUb inside the sample [70]. The versatility and simplicity of MC generation models favor their universal application even in complex geometrical cases [7,56]. To obtain accurate results, however, they may demand long computation times. Since it would complicate a fast analysis if the same task had to be repeatedly solved for equivalent experimental conditions on bulk materials, an empirical three-component Gaussian expression has been accurately fitted to MC results once calculated in the beam voltage range Ub = 2 ... 50 kV and semiconductor materials with average atomic number between Si and GaAs [38,61,70]. Furthermore, for the exact modelling of EBIC and CL signal from the homogeneous matrix region (see below) as well as the defect contrast profile area of a surface-parallel dislocation [27], only the well-known depth distribution gz(z;Ub) (see (6)) and no explicit calculation of q(r) is required. For these reasons, the effort of repeated MC simulations is often unnecessary, and it can be separated from the actual problem of signal modelling. This fact is sometimes ignored in the literature [9,31,54].
    Finally, by choosing the appropriate light generation function, the considerations of this paper may be readily applied to light beam induced current (LBIC) and photoluminescence (PL) which might be very useful in view of the recent progress in scanning PL investigations of dislocations [68].
    In order to perform an EBIC experiment, the sample must contain a potential barrier to separate the generated electron-hole pairs such as the surface Schottky barrier of Figure 1 or a p-n junction so that the major part of the EBIC signal is given by the diffusion current towards the edge of the depletion region rb [11]:
An additional drift current contribution may originate from the separation of carriers generated inside the depletion layer.
    The spectral CL signal (photon flux leaving the sample surface) collected by an ideal spectrometer [22]
is given by the integral of the radiative recombination rate over the sample volume s corrected by losses due to spectral optical absorption (h) and total reflection at the sample surface for escape angles larger than the critical angle c. Q(h) denotes the relative internal spectral distribution of the recombination radiation. In the case of panchromatic, spectrally integrated CL experiments, (5) remains correct if "effective" parameters for quantum efficiency  and absorption  are introduced.
    An important advantage for the calculation of the matrix signals from a defect-free region was the introduction of a unified formalism [21] being valid for all sample geometries with rotational symmetry. Induced current and luminescence signals are expressed in terms of a universal function describing the specific exponential losses by diffusion or absorption and the effect of an arbitrary generation depth distribution:
For example, we obtain a simple formula for the CL signal from a semi-infinite homogeneous sample with a dead layer of thickness zT at the surface (S = vS /L,  = /cos )
Similar expressions are derived for the surface-parallel Schottky or p-n EBIC signal with explicit consideration of metal and/or depletion layers as well as for layered structures [21,43]. Many other literature results such as [10] could be covered more easily within this framework as well. It should be noted that the so-called normal collector geometry with a p-n or heterojunction perpendicular to the surface has a more complicated solution which will not be discussed here (see, for example [13,18,42,44]).
    In connection with the calculation of the matrix signals using the unified formalism, the concept of information depth zI and information radius rI, i. e. the range where 95 % of the CL radiation originate from, has been developed [20,22]. It was found that zI  4 µm for  > 104 cm-1, L > 1 µm nearly independent of Ub. Other ways to determine the lateral image resolution in EBIC and CL have been proposed in [12,51].
    For comprehensive studies on the formation of the defect contrast from dislocations it is necessary to take into account the intrinsic nature of dislocation recombination, effects due to interaction with surrounding point defects as well as geometric contrast factors. Generally, defects are supposed to change the local recombination properties of the sample. Hence, their electric activity resulting in a recombination contrast has to be considered with respect to bulk recombination rates. The knowledge of matrix signals and corresponding parameters is therefore a general requirement for a quantitative analysis of the defect contrast. In our fundamental considerations we will mainly refer to the model case of a surface-parallel dislocation applicable for many both misfit and glide dislocation geometries (Figure 2). Beyond the basic configurations of single surface-parallel or -perpendicular dislocation lines, the large variety of possible situations such as inclined, curved, or composed defect features should be the subject of numerical modelling (cf. below).
    In the volume recombination model (VRM), the dislocation is characterized by a cylindrical region D where the total lifetime ' differs from the bulk value . The defect-induced recombination strength [11] is given by
The radius rD of the dislocation cylinder may be first interpreted as a "capture cross section" but one can also try to infer this region from physical dislocation properties such the extension of the core region, strain field or the space charge region of a charged dislocation. However, it can be shown that for rD « L the shape of the contrast profile of a surface-parallel dislocation line is independent of rD. In this case,  and rD cannot be determined separately but form together a defect strength  [412,45] (cf. (13)). On the other hand, impurity decoration or a gettering-induced denuded zone may cause a larger extension of the defect-related region as shown e. g. for GaAs in an early work by Balk et al. [3]. In such a situation or if specific defect bound emission occurs, the radiative recombination can be directly affected. This is considered by introduction of a second defect cylinder Dr of radius rDr with modified r' and r = r/r' - 1, respectively. In principle, this model is able to describe the well-known "dot-and-halo" contrasts.
It is noted that in the alternative "surface" recombination model [34] the dislocation is represented by a recombination velocity at the cylinder boundary instead. This model may yield partly analogous results as the VRM, however, it will deviate if defect and generation region overlap each other - a common experimental situation - since this would result in an unrealistic 100 % contrast contribution from this region. These difficulties could be overcome by the introduction of an "effective" radius [34].
    A defect contrast profile, i. e. the linescan over the defect, is given by
where  is the lateral beam position relative to the defect and I0 the matrix signal far away from it. Usually, the central value c(0) is denoted "the (maximum) contrast value" irrespective of its sign (here defined negative for a dark and positive for a bright image contrast). Furthermore, the profile half-width (FWHM) and the contrast profile area [15,27] may be used to characterize the contrast.
    The CL defect contrast has been derived [49,59] as
Here, j0CL(z) stands for the defect-free CL signal from a point source located at depth z. According to the cylindrical regions in the VRM, it generally consists of two parts. The first part arises from the change in the total lifetime and is analogous to the EBIC contrast expression not written here. The second, CL-specific term results in an exclusive luminescence contrast contribution caused by the change of r at the defect provided the total lifetime  remains unaffected by the variation in r.
    Obviously, the central task of the contrast calculation is the determination of the carrier density q(r) in the sample containing the defect. It is related to the defect-free case q0(r) by the Dyson integral equation
    A common method for the analytical solution of (11) is perturbation theory. In first order [11], the undisturbed q(r) = q0(r) can be used for the calculation of the contrast of weak defects. q0(r) is known analytically for uniform sphere generation [22] and can be calculated half-numerically for a realistic generation in a half-infinite sample with S   [28]. Although nowadays the entire contrast simulation could be performed numerically [9,31,52,53,69], analytical methods are of great value. Besides their smaller computational effort, they allow better insight into contrast formation and properties. In this way, it was realized that the contrast of a surface-parallel dislocation may be written as [28,60]
that means in terms of products of a function c* and a corresponding defect strength  or r. We note that if r = 0, both EBIC and CL contrast profiles are given by the same profile shape function c** and only the contrast amplitudes differ according to f0EBIC and f0CL.
    In first order perturbation theory we obtain for the total and radiative defect strength, respectively,
The further perturbation expansion has been evaluated in [45] leading to modified defect strength expressions. It was found that the series converges for (1) < 1.2 only. The convergence criteria were discussed in [23]. However, the theoretical contrast description must be able to cover a wide range of defect strength values. Strongly recombination-active defects cause a noticeable change in the excess minority carrier density giving rise to a complex non-linear contrast behavior with saturation of the diffusion controlled recombination for high activity. Several approaches were developed for a contrast solution valid beyond the convergence domain [14,47,62] as illustrated in Figure 5. Therefore, the problem of calculation of CL and EBIC contrast from a surface-parallel dislocation may now be considered as completely solved.
    Finally, we can see from (12 a) and (12 b) that for r = 0, rD « zD,L the contrast ratio cEBIC/cCL is given by f0EBIC/f0CL being an exact measure of the depth position zD of the surface-parallel dislocation line, dependent on the matrix parameters only [49]. This property caused by the complementary response of EBIC and CL signal to the spatial propagation of charge carriers and recombination radiation is of great practical use for the determination of defect depths and a complete contrast analysis requiring the knowledge of zD.
    For a surface-perpendicular dislocation, the theorem of reciprocity allows a rigorous calculation of cEBIC as an integral expression for arbitrary generation [46]. It is an elementary property of Green's function3 which connects the EBIC signal (the diffusion current) in the case of carrier generation by a point source at r with the reciprocal case of homogeneous injection of  carriers over the EBIC barrier to produce a minority carrier distribution n(r) in the sample:
It was shown that contrary to the surface-parallel line defect, for very low values of Ub (electron range Rp  2 rD) (1) is not a suitable recombination activity parameter since various combinations of /' and rD give divergent contrast curves and profile half-widths. Although this particular half-width behavior might be helpful for a direct estimate of the defect radius rD, it has not been proved experimentally yet. It may be expected that depletion region and surface recombination effects will also influence the EBIC contrast. Therefore, we will not further discuss this situation in the paper. The reciprocity concept is not simply transferable to the case of CL. In order to treat this case as well as other dislocation geometries such as inclined dislocations [69], new findings are expected from results of numerical calculations.

Simulation Results

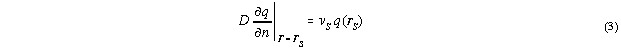
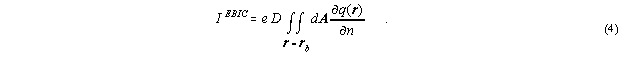
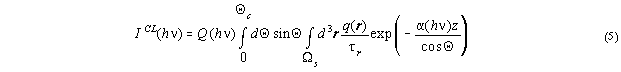
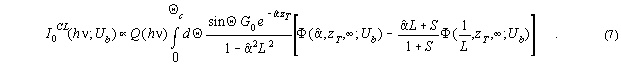
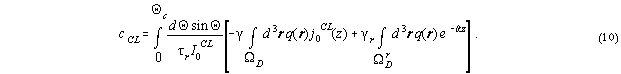
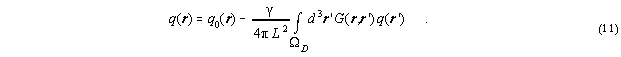
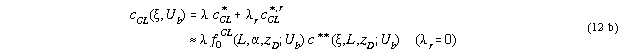
    Results of simulations of the matrix signals I0EBIC and I0CL from defect-free samples can be found in [24,37,73]. It was shown that the beam-voltage dependent Schottky-EBIC signal I0EBIC(Ub) plotted for constant G0 is sensitive to the diffusion length as well as to the metal layer thickness zm. For the surface-parallel p-n geometry and layered structures or inhomogeneous material, depth profiles of L can be extracted [16]. The corresponding CL signal depends on S and zT but it is dominated by the diffusion length L and the optical absorption (h) or , respectively. Both parameters exhibit a strong correlation in the signal. In order to prevent the evaluation of ambiguous values, the maximum position Ubmax of I0CL(Ub)/G0 may be used to estimate  [24] if L is known from other experiments such as simultaneous EBIC measurements, for instance using a thin transparent Schottky contact (zm  10 nm) on the surface. The CL mode also permits to locate lateral and vertical inhomogeneities or buried interfaces if a suitable model can be applied [8,35]. Normal-collector EBIC line profiles allow to determine the diffusion lengths Ln and Lp on both sides of the p-n junction as well as S [13,18].
    CL and EBIC dislocation contrasts show a characteristic behavior as a function of the beam voltage. The typical behavior for a surface-parallel dislocation is illustrated in Figure 3. Since the contrast value is strongly influenced by geometric factors such as generation range Rp(Ub) and defect depth zD, the evaluation of the recombination activity is only possible if these parameters are known. If both EBIC and CL contrast can be measured, the contrast ratio cEBIC/cCL yields zD. Consequently, a combined CL/EBIC experiment at one given beam voltage would be sufficient to determine . However, a complete measurement of the c(Ub) curve yields more reliable data, and the depth position may then also be derived as an additional fit parameter (cf. Figure 8). Arising from the joint profile function c**, profile half-widths of CL and EBIC contrast are identical. Plotted in Figure 3 (b), they do not exhibit a minimum as predicted for uniform sphere generation [11] but rise from a nearly constant value with increasing Ub. For shallow dislocations, the gradual decrease at high Ub beyond the maximum half-width is a special feature of the realistic generation in accordance with [53] and own, unpublished experimental data from GaAsP.
    An example for the influence of the matrix parameters on the contrast profiles is shown in Figure 4. It is seen that a variation of the bulk diffusion length results in rapid changes in maximum contrast and profile half-width predominantly in the range L  1 µm. This behavior may be important for the interpretation of temperature-dependent contrast measurements on III-V materials as discussed below. Only for large L > 5 µm (typical for Si), the influence of the diffusion length is small and a constant half-width is found.
    We expect from (12 a) that may be obtained from a comparison of the experimental contrast and the theoretical profile function which can be calculated if the other parameters are given. However, the defect strength determined in this way cannot grow arbitrarily high. Even if a defect is considered as a "black sphere" (' = 0), the contrast will not range above a saturation value [14] due to the defect-induced local reduction of q(r). An example for this contrast property is shown in Figure 5. The first order approximation (13) is applicable only for weak defects (1) < 0.15. Although there is some variation between the various other models they all show basically the same saturation behavior for high  (including the sum of the perturbation expansion which actually holds for (1) < 1.2 only). It should be further noted that the shape of the contrast profile remains unaffected by the  value.
    It is thus concluded that  has to be generally interpreted as a non-linear defect strength being the appropriate parameter for the quantitative description of the specific dislocation recombination activity in CL/EBIC experiments. A direct relation to the defect-induced lifetime ratio or recombination rate is only possible for the case of a weak defect or otherwise if the degree of deviation from linearity is known, for instance if an estimate for rD can be given [69].
    During the last years, increased efforts have been made to develop numerical simulation models for the calculation of the excess carrier distribution, CL and EBIC signals, and the defect contrast [9,31,36,52,53,69]. Numerical methods have the advantage of being able to deal with defects with irregular shapes and characteristics.
    In the framework of the above given model, arbitrary defect and sample geometries may be treated by a finite difference scheme. A first result for the numerical simulation of q(r) in the presence of a surface-parallel dislocation line using the realistic generation model is presented in Figure 6. For these calculations, the FIDISOL/CADSOL solver is conveniently applied [58], a program package developed for the solution of boundary value problems for systems of partial differential equations of various types using a nonequidistant grid and varying order of consistence. Grid size and spacings have to be chosen carefully in order to minimize numerical errors and to model the defect with sufficient precision. It is clearly seen from the results in which way q(r) is modified by the action of the dislocation. For small defect strengths ((1) = 0.89), the carrier density is reduced but its original shape is maintained. This explains why in this range the undisturbed distribution q0(r) may be used in first order analytical calculation. Only for higher defect strength values, the local distortion of q(r) around the defect becomes significant. CL and EBIC signals and contrasts may be reproduced by numerical integration/differentiation of the carrier density choosing either the full calculation by eqs. (4),(5) or the contrast formula (10).
    Despite of the fast advances in available computing capacity, a full numerical treatment of the spatial carrier behavior still needs high memory and time requirements. The general problem of the solution of the coupled basic electronic and transport equations is rather extensive and closely related to complex tasks in device simulation [36,64]. We conclude here that these methods exhibit a big potential, however, it should be considered which cases really require a numerical treatment. The symmetry of the problem as well as the fact that the calculation of the contrast (10) requires q(r) only inside the defect region should be taken into account. Furthermore, alternative ways in contrast modelling such as finite element techniques could be used where body-oriented grids can be more easily adapted to defect and generation geometries.

Experimental Details

    For the performance of CL and EBIC experiments, the SEM should permit a beam voltage variation from below 1 kV up to high values of at least 40 kV. The range between 40 and 50 kV which is accessible using our SEM Tesla BS 300 is, however, hardly offered by commercial suppliers today. The electron gun (preferably LaB6 cathode) and optics must be able to supply small stable beam currents to ensure low injection conditions with beam powers of Ub Ib < 20 µW over the whole Ub range. Beam currents are measured using a Faraday cup. Small luminescence intensities require an efficient, optimized collection system with a parabolic or elliptic mirror and photomultiplier or Si diode detectors. For the spectroscopic CL investigations, we use narrow band pass filters or a grating spectrometer system (CL302m by Oxford Instruments). Lock-in amplification, optical multichannel analyzers, or Boxcar technique in combination with digital scan for EBIC and panchromatic or monochromatic CL line profile recording as well as image processing are widely available now. The temperature-dependent studies are performed under vacuum conditions of better than 10-4 Pa in the temperature range between 5 and 300 K in the SEM equipped with liquid helium or nitrogen cooling stage (CF 302 by Oxford Instruments in our setup).
    Samples are epitaxial and bulk material of (001) or (111) orientation. For glide dislocation generation, plastic microdeformation is achieved by Vickers indentation at room temperature with typically 0.05 to 0.4 N load to activate the principal {111}<110> glide systems. For GaAs, it is followed by a thermal treatment of 15 min at 400 °C. The qualititative characterization of the defect configuration is performed by means of crystallographic considerations of the dislocation rosette geometry or by TEM investigations. Semitransparent Au Schottky contacts on n-type III-V sample surfaces are produced by vacuum evaporation using standard preparation methods. For ohmic contacts, an Au-Ge eutectic on the sample backside is annealed at 350 °C for 10 min.

Experimental Results

    It has been demonstrated in a number of papers how material parameters such as L, , and Q in compound semiconductors can be determined from fits to EBIC and CL data of homogeneous sample regions based on the results of the theoretical simulation. In order to investigate the recombination mechanisms in optoelectronic materials, the parameter variation with doping level in bulk n-GaAs (n0 = 7 · 1016 to 3 · 1018 cm-3) [39,55] and GaAsP was studied using EBIC and panchromatic CL. The diffusion length L(n0) does not always show a systematic doping dependence. However, because of r ~ n0-1 and L2 ~  (D = const.) the relation for the relative quantum efficiency Q(n0) ~ n0 L2 was shown to be in good agreement with the experiment. It could be verified that the recombination is dominated by non-radiative processes   nr except near the maximum of Q at n0  1018 cm-3 where r and nr become comparable. Panchromatic CL measurements allow to determine only an effective absorption coefficient . It decreases with doping according to the Burstein-Moss shift of the absorption edge to higher energies relative to the spectral position of the CL band.
    More detailed information about material properties may be derived from spectrally resolved CL data I0CL(h;Ub) [29]. Figure 7 (a) shows an example for the monochromatic beam voltage dependencies converted from CL spectra of p-GaAs measured at constant beam power Ub Ib = 20 µW. They display a clearly variable shape with photon energy h. The spectral absorption edge (h) may be accurately determined by the fit (Figure 7 (b)). Because of the large electron diffusion length L = 4.5 µm in the p-type material as determined by EBIC, the CL intensity increases rather slowly with Ub. Therefore, the absorption-related signal maximum is expected beyond 50 kV in this example. However, due to the large extension of the diffusion region, the absorption still plays a significant role even at 10 kV causing a low-energetic shift of the CL spectrum by about 20 meV compared to the internal spectral distribution Q(h). This emphasizes the advantage of spectral CL experiments for the determination of the absorption edge and self-absorption correction.
    For the quantitative investigation of single defects, the conception of combined beam-voltage dependent CL and EBIC contrast profile measurements has been successfully applied to dislocations in GaAs, GaP, and GaAsP by the authors [59,60,61,62]. Other workers [32,33] have also investigated either cEBIC(Ub) or cCL(Ub) without detailed evaluation of the recombination activity. Figure 8 displays results of contrast measurements from a process- or stress-induced surface-parallel dislocation in the near-surface p-type region of a GaAs p-n diode structure. Using the realistic generation function with depth-dependent half-width of the radial distribution gr(r,z) [38], excellent fits to both the maximum contrast and the contrast profiles were achieved over the whole beam voltage region. The dislocation depth is in agreement with the value given by the EBIC/CL contrast ratio. Obtained differences between defect strength values derived from EBIC and CL, respectively, discussed in [61] could be attributed to a locally changed background CL intensity due to the gettering activity of the dislocation.
    A comparison of CL defect contrasts from an edge-type misfit dislocation in GaAs0.38P0.62 and a screw-type glide dislocation in GaAs is shown in Figure 9. Both defects exhibit the same basic homogeneous, dark contrast appearance. The maximum contrasts as well as the profile half-widths between 1.5 and 3.5 µm are in good correspondence to the results of the model calculations with minimum FWHM for both examples. Spectroscopic CL investigations show no variation in the spectral distribution from defect and matrix regions. The observed noticeable differences in recombination activity between grown-in defects and dislocations freshly introduced by microdeformation should therefore be attributed to the intrinsic dislocation behavior or to the influence of a rather weak impurity or point defect decoration. These two cases can only be distinguished by further experiments such as recombination-kinetic studies (see below). Strong decoration effects, however, may be excluded here. It is noted that a quantitative evaluation of the recombination activity is only possible by using the fitted  values but not by comparing the contrast values which are strongly dependent on Ub and zD.
    Representative defect strength results are compiled in Table 2. A wide range of  values is obtained from experiments on various dislocation configurations. It should be noted that data intervals given in the table do not represent the experimental or analysis error but indicate the  variation along a dislocation line or on several dislocations in a sample. This reveals the influence of the interaction or decoration with point defects as well as others factors such as inhomogeneous bulk doping. Especially, a large local variation is found for dislocations introduced by Zn diffusion/thermal stress in p-GaAs. Furthermore, the data clearly confirm the typical occurrence of smaller defect strengths  < 0.95 of fresh glide screw dislocations compared to grown-in, weakly decorated misfit dislocations ( > 1.26) in the direct gap III-V materials GaAs and GaAsP.  values for glide dislocations in GaAs:Si calculated from [69,72] agree well with our results although these results were obtained on a different geometric configuration. They also show the trend of somewhat higher recombination activity for an  glide dislocation. Several authors [19,65,72] found a slightly stronger CL contrast on - than on ß-dislocations in n-GaAs and vice versa in p-type material. Conclusions were drawn concerning the defect-related electronic gap states for these dislocation types. Only relative recombination activity data were given. Recently, essential differences in the recombination activity of polar glide dislocations have been observed in CdTe [40,63]. There,  dislocations show a localized, defect-related sub-band-gap CL radiation at low temperatures whereas ß dislocations are characterized by the usual non-radiative recombination contrast. Since absolute  values are available from a small number of papers only, further systematic and comparable defect strength measurements remain a current task of combined CL/EBIC experiments.
    New and more detailed insight into the defect recombination mechanisms are expected from temperature-dependent contrast experiments [19,65], especially in the low-temperature region below T = 77 K where very few results have been published in the past [17,66]. We have performed panchromatic and spectrally resolved CL experiments between 5 to 300 K. Different behaviors of the dislocation recombination have been found in the III-V materials GaAs and GaP and the II-VI semiconductor CdTe. For the interpretation of these experiments, the defect-related recombination has to be considered in context with the temperature dependence of the bulk recombination rates. Especially, the diffusion length may exhibit a significant variation with temperature [5,17,19]. For the present analysis, a basic temperature-dependent recombination-kinetic model including both defect-bound and bulk radiative and non-radiative channels is proposed.
    Figure 10 (a) shows typical results of CL contrast measurements as a function of temperature from a surface-parallel misfit dislocation in n-GaP. Contrasts of dislocations perpendicular to the surface behave essentially in the same way. It is seen that as the dark contrast varies rather little with temperature above 70 K, it diminishes quickly below 50 K. In this material the bulk diffusion length L has been found to be only weakly temperature-dependent. This is also reflected by a nearly steady contrast profile half-width of about 6 µm (c**  const.). Followed from (10) and (12 a), in this case the contrast value may serve as a direct measure for the defect recombination rate RD:

From the luminescence intensity I0CL(T) of the defect-free matrix it is concluded that the bulk recombination is well described by a thermally activated multiphonon process nr ~ exp(EA/kT) with EA = 47 meV (cf. [67]) whereas the radiative lifetime r is supposed to be temperature-independent. With the assumption RDr ~ ID ~ p the temperature dependence of the defect-related lifetime D can be estimated (Figure 10 (b)). It changes by more than five orders of magnitude over the investigated temperature range which is interpreted as a distinct variation of the defect-induced recombination properties. The Arrhenius plot implies the participation of thermally activated capture of carriers into shallow defect states and subsequent non-radiative recombination. These states should be of extrinsic rather than intrinsic nature due to the similar temperature dependence of  and D. In principle, one should be able to describe such a behavior by a model similar to that developed for EBIC on dislocation in Si [71].
    On the other hand, on GaAs the observed defect contrast behavior hints at a more complicated correlation between the temperature dependence of dislocation recombination activity and the effect of altered material parameters. Measurements of an individual threading dislocation contrast in the branch of a microindentation glide rosette show a CL contrast increasing only slightly by 3 % between 300 and 5 K (Figure 11) (see also [17,19]). Since the diffusion length in GaAs is a strong function of temperature, this effect alone would cause a rapid change in contrast (cf. the theoretical example of Figure 4). Indeed, we also observed a clear increase in the contrast profile half-width from 2.7 µm at T = 5 K to 4.2 µm at room temperature. Therefore, it is inferred that the temperature dependence of defect strength and diffusion length cancel each other to produce only a weakly temperature-dependent contrast. Eliminating the temperature variation of L(T) and (T), the detailed analysis [63] yields a decrease of the actual defect recombination activity ~ 1/D with falling temperature. The deduced thermally activated recombination activity contradicts the interpretation in [17] of quenching of thermal carrier re-emission from a shallow acceptor level.
    The results emphasize the relevance of a comprehensive contrast model with inclusion of all material and geometry parameters. This will allow us to combine the straightforward recombination-kinetic analysis with the spatial modelling of the carrier behavior as performed earlier for the room temperature experiments.

Conclusions

    The importance of combined SEM-CL/EBIC investigations for the identification and quantitative characterization of recombination-active individual defects in compound semiconductors has been demonstrated. New developments such as advanced realistic analytical and numerical modelling of the defect contrast and investigations in the low-temperature range have been illustrated. The detailed interpretation of derived defect and recombination strength values and the temperature dependence of the material and defect recombination rates remains a challenge in future investigations. For experimental defect studies, the defined preparation of clean or decorated dislocation configurations is a major issue. SEM injection conditions, especially in the low-injection regime, should be carefully considered since it is known that both bulk and defect parameters may be influenced by the carrier injection level and density [2,68,71].
    Renewed interest is directed to effects of defect-related radiative recombination as it has been observed in recent experiments on polar glide dislocations in CdTe at temperatures below 100 K where it gives rise to bright CL contrasts originating from the Te(g) segments [40,63]. An activation energy of 11 meV for the defect emission determined from the temperature dependence of the local CL spectra is well described by defect-bound excitonic recombination [30]. A further structural and quantitative analysis is in progress.
    Finally, other EBIC contrast mechanisms not discussed here such as charge separation at the potential barrier of a charged dislocation connected with one-dimensional conduction along the dislocation line [2,17,26] may also be taken into account, especially at low temperatures.

Acknowledgements

    This work was partially supported by the research grant no. 1557A0024 from the Ministerium für Wissenschaft und Forschung des Landes Sachsen-Anhalt and a PROCOPE project support no. 312/pro-gg from the Deutscher Akademischer Austauschdienst.

Discussion with Reviewers

T. Sekiguchi: As for the experimental point of view, the excitation energy (E) dependence is somewhat ambiguous. It comes from the different behavior of total number of generated carriers and their density on the excitation energy (E). If we accept the uniform generation sphere model and the generation radius is proportional to E1.75, the excess carrier density is proportional to E-4.25, while total number of excess carriers to E. Which parameter is required to be constant, the density or the total number of generated carriers?
    Please suggest us how experimental procedure should be done.

Authors: From a physical perspective, the experiments should be performed at a small constant excess carrier density in the low injection range at the defect or in the sample region to be investigated. However, the exact evaluation of the excitation level inside the sample is not straightforward. Values for the carrier density q calculated on the basis of simplified generation models can only be a rough estimate. q(r) may vary by several orders of magnitude over r and the material parameters L and D. Usually, the maximum of the q(r) distribution must be calculated for the correct semiconductor parameters and realistic generation to determine the injection level.
    Experimentally, the validity of the low injection regime should be proved for each specimen by inspecting the linear variation of the CL and EBIC signal with beam current Ib at a given beam voltage Ub = E/e. Also, the signal should be equal for focused and defocused beam, respectively. In practice, beam voltage dependent experiments have been performed at constant beam power P = Ub Ib which must be small enough to fulfil the low injection condition even for the smallest Ub (typically P < 5 ... 20 µW) [24,29,39]. The obtained CL and EBIC signals are then normalized to the total generation rate G0 being approximately constant except for a weakly Ub-dependent backscattering correction. It should also be kept in mind that the low injection condition may be different for defect recombination paths. This can be checked by measuring c(Ib) at Ub = const.

T. Sekiguchi: Do you have some idea about the value of  and the physical parameter of dislocation? ( Table 2)
Authors: As the defect strength  is given in first order approximation by (13), it depends on the ratio of /D of lifetimes for defect and matrix recombination paths as well as on the dislocation radius rD. The further interpretation of  requires the implementation of a dislocation model which calculates these quantities on the basis of the recombination kinetics. Various models for defect recombination controlled by the dislocation charge [71] or based on the Shockley-Read-Hall recombination statistics [76] have been successfully employed for Si. However, they should be applied to the extracted defect strength rather than to the contrast as it has been well demonstrated in one of your recent papers [77]. The development of recombination-kinetic models for dislocations in compound semiconductors is the subject of current investigations [63,65]. Usually, their application will require temperature or beam current dependent contrast measurements. The recombination mechanisms are expected to be more complex than in Si, for example if excitonic transitions are involved.

J C H Phang: It has been shown in [75] that various semiconductor parameters may be extracted entirely from CL experimental data by varying the incident beam energy. Is it necessary to use both CL and EBIC data to determine the parameters as suggested in Table 1?

Authors: The correlation of L and  in the Ub dependence of the CL matrix signal means that the global minimum of the sum of least squares in parameter space is a very shallow one. You have demonstrated that it may still be possible to find this minimum by using sophisticated and extensive minimization techniques. However, it is doubtful if this can be achieved for any limited set of realistic data couples with both statistical and systematic errors. For example, it is possible to fit the data in Fig. 8 of [75] using L and  couples being about four times larger than the values given (thereby adjusting the other parameters as well) which leads to an increase in the sum of least squares of only about 0.1 %. Therefore, one should also look for alternatives to determine L from CL data, for example, using the contrast profile half-width. It is obvious, however, that both CL and EBIC experiments are needed if the total as well as the radiative defect strengths  and r are to be characterized, for example due to the occurrence of a defect-related spectral CL emission.